Возможен ли разговор двух Ардуин на КВ?

Возможен ли разговор двух Ардуин на КВ?

Сегодня мы будем решать задачу (ну или хотя бы попытаемся это сделать) приёма информации, переданной по эфиру, силами простейшей Ардуины. Автономно, без компьютера.

Также оговоримся, что радиоканал расположен в пределах КВ диапазона, что подразумевает радиус действия порядка 1000 км при мощности в пару Ватт даже в случае самодельной железяки. Звучит круто, но в отместку принятый сигнал будет лежать глубоко под шумами.

Досадно, но воспользоваться готовым алгоритмом какой-нибудь цифровой моды не получится. Не те у Ардуины ресурсы. Библиотека для передачи «цифрой» в неё ещё влезет, а вот принять ту же «цифру» обратно уже не выйдет.

Понятно, что упоротых самоделкиных такие мелочи не остановят, ибо всего-то нужно изобрести велосипед. Чем можно заниматься долго и вдохновенно.

Очевидное.

Чтобы почувствовать нечто маломощное за сотни км, лучше всего этому маломощному излучать когерентный сигнал, причём поочерёдно на нескольких частотах (FSK модуляция). Так работают хорошо продуманные WSPR, QRSS, и прочие затейливые штуки с хождением милливаттами за радиогоризонт через ионосферу.

Надёжно определить наличие или отсутствие сигнала на одной или нескольких частотах можно лишь спектральным методом (преобразование Фурье в одном из вариантов). Но скромные аппаратные возможности Ардуины не позволят обсчитывать спектры быстро. Даже за WSPR Ардуине не угнаться.

Посему изобретаемый велосипед должен быть весьма низкободовым, а сама процедура коннекта неторопливой. И по-любому лучше обойтись без использования таймфреймов, без которых в последнее время как-то вот никак.

Прикидки.

Попробуем оценить, что получится реализовать на прозаической Ардуино Нано.

Если рассматривать спектр на выходе приёмного тракта самодельного трансивера, принимающего голос в SSB, то при громогласном разговоре в канале можно увидеть такую картинку:

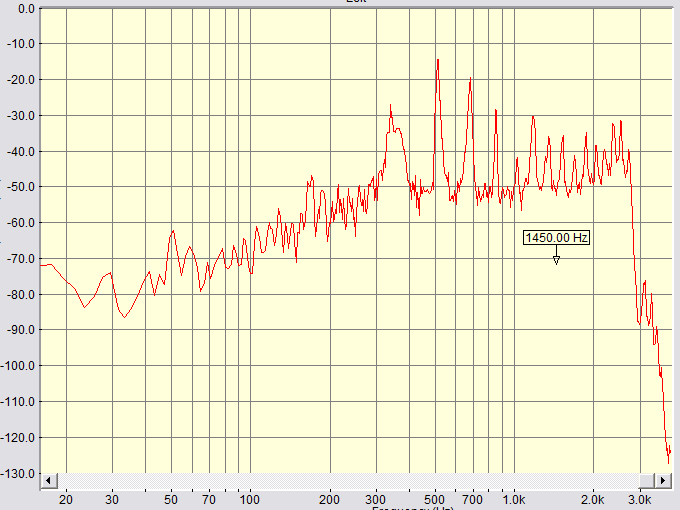
Местным автором применён тракт Уивера, поэтому завал АЧХ выше 2700 Hz довольно резкий, и можно считать, что правее 3 kHz никакого сигнала уже нет.

Чтобы оцифровать сигнал в полосе 0-3000 Hz, частоту сэмплирования придётся взять вдвое выше максимальной частоты оцифровываемого сигнала, то есть 6 kHz. Период сэмплирования превышает 166 µs, чего более чем достаточно для исполнения ардуиновской процедуры analogRead штатным методом (120 µs), и не придётся извращаться с вариантами быстрого чтения, обычно проистекающими с потерей разрядности. Да, понадобится запись сэмплов по таймеру, но это организуется просто.

Пока вроде всё хорошо.

Теперь нужно выбрать количество отсчётов так, чтобы спектральное разрешение составляло хотя бы 10 Hz. Мы все с детства люто ненавидим формулы из учебников, поэтому на маленькой картинке приведён скрин с софта SpectraPLUS, где FFT Size, кратный степеням двойки, для нашего случая равен аж 512 отсчётам.

Далее будем смотреть в сторону разных способов реализации алгоритма быстрого преобразования Фурье.

1. FIX FFT.
   Вариант, обычно и используемый в разных любительских самоделках.

   Быстрый, может работать с 256 сэмплами даже на Ардуино Нано. Однако данные пишутся в массив типа char, то есть с понижением разрядности до 8 бит. Для оцифровки звука данная библиотека совершенно непригодна, даже сильный сигнал оказывается заметно зашумлён. Дёргать столбики на индикаторе спектра годится, но не более того.

2. arduinoFFT
   Это уже полноценный вариант, оперирует массивами типа double, который в Ардуинах равносилен типу float. Оцифрованный сигнал теперь гладенький и красивый, но больше 128 отсчётов в «народную» Ардуино Нано не помещается. Для наших минимальных 512 отсчётов потребуется Мега.

3. Алгоритм Гёрцеля
   Рабочий массив с данными у него вдвое меньше по объёму, и, что самое главное, число отсчётов больше не привязано к степеням двойки, позволяя выбирать спектральное разрешение напрямую.

   Так, при частоте дискретизации (она же частота сэмплирования) 6 kHz и желаемом спектральном разрешении 10 Hz нам понадобится 600 отсчётов. Даже Ардуино Нано такое выдержит.

Последний обстоятельство решающее, но в немногочисленных библиотеках либо примерах их использования нет никакого единства по кодировке тела алгоритма. Всё с вариациями. Наиболее близкое к формулам из Википедии сыскалось тут - местный автор взял этот документ за основу.

Утечка спектра.

Если подсунуть алгоритму Гёрцеля сгенерированные данные, согласно которым звук плавно меняется от 950 до 1050 Hz, а контролируются частоты 990, 1000 и 1010 Hz, при спектральном разрешении 10 Hz, то такой скетч выдаст в плоттер по последовательному соединению довольно странную картинку:

На контролируемых частотах действительно рисуются пики, когда сигнал тех частот достигает, однако по бокам у каждого такого пика виден целый выводок артефактов. И это нехорошо, ибо сильный сигнал чуть в стороне может дать всплеск на контролируемой частоте, то есть ложный сигнал.

Если почитать про утечку спектра (так это зовётся) в подобающем месте, там встретится очень похожая картинка:

Действительно, нельзя просто так выдрать произвольный кусок синусоиды при сэмплировании, причём со случайной фазой на концах отрезка, чтобы она при этом осталась, как живая.

Нечто подобное мы видим на «водопаде» связного софта, когда тональная посылка (например, телеграфная, CW) начинается или заканчивается - по горизонтали от этой точки в стороны разбегаются всполохи. Чтобы такого не случалось, манипулирование производится особым образом.

Как бороться с утечкой спектра, написано в документе, где предлагается перемножать оцифрованный сигнал в виде массива сэмплов на ту или иную оконную функцию, обращающуюся в середине в единицу, а по краям в ноль.

Множество таких оконных функций там же и перечислено, с указанием формул и весовых коэффициентов. Но проще взять готовый код из выше упомянутой библиотеки arduinoFFT. Для вот такого скетча плоттер Arduino IDE по последовательному соединению нарисует замысловатую картину:

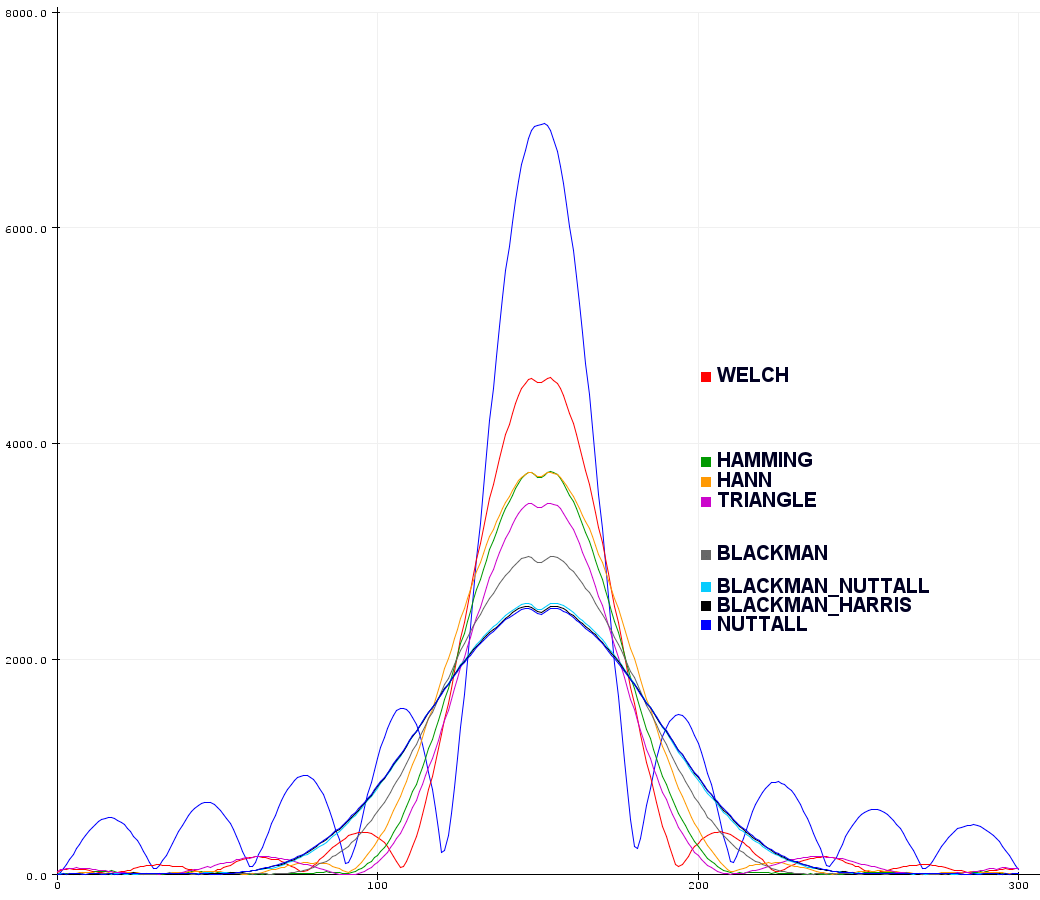
Пик самой большой амплитуды и с артефактами по бокам - исходный сигнал без коррекции оконными функциями, в сравнении с наиболее известными оконным функциями, применёнными к исходному сигналу.

Скажем прямо, пользы от всего этого многообразия нет никакой, можно оставить только первые две. Это WELCH и HAMMING. Может быть, HANN:

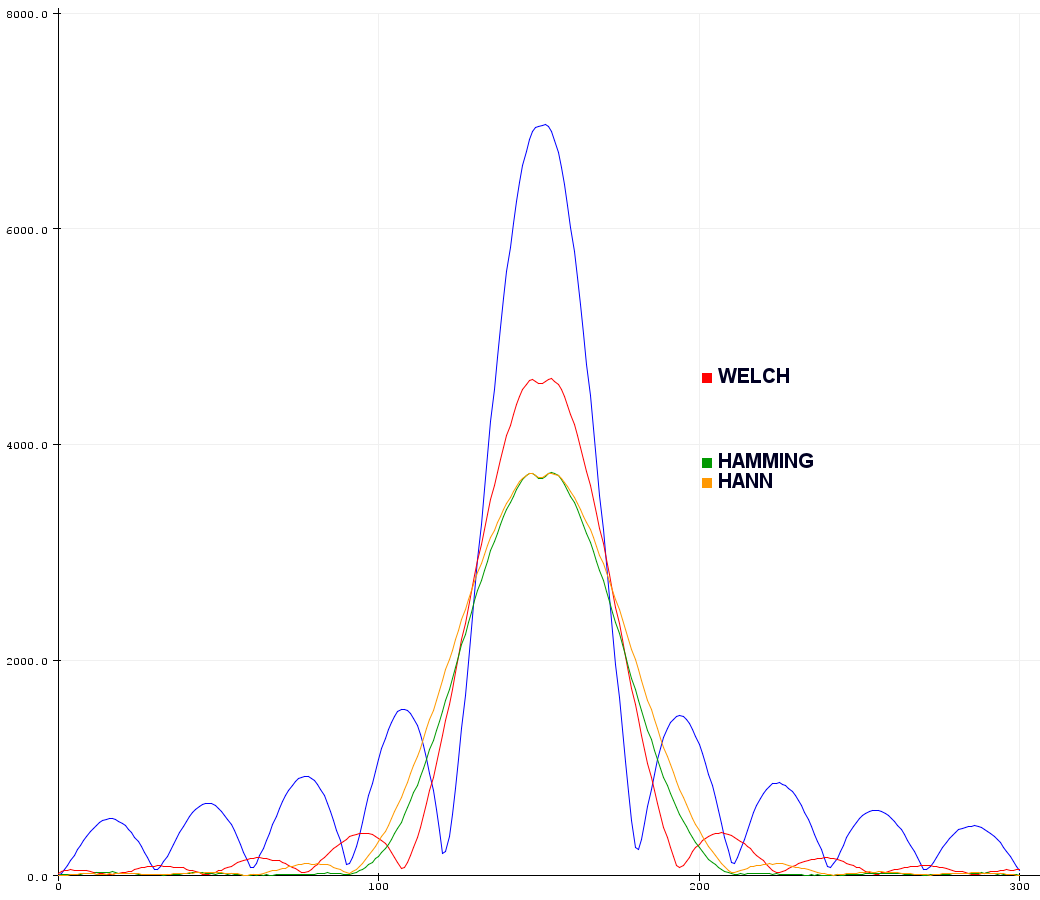
Критерий понятен - оконная функция должна эффективно гасить артефакты по бокам пика, обеспечивать максимальную амплитуду в центре, и не сильно уширять сам пик. На большом сигнале оконная функция HAMMING идеальна, и, как правило, в спектральном и связном софте с «водопадом» используется именно она.

Но на малом сигнале, когда важно сохранить максимально возможную амплитуду пика, желательно применение оконной функции WELCH.

Правда, если внимательно читать Википедию, про прямоугольное окно (отсутствие оконной функции вообще) сказано, что оно «хорошо различает компоненты одинаковой амплитуды, даже когда частоты близки, но плохо различает компоненты разной амплитуды, даже когда частоты находятся далеко. Прямоугольное окно также способно выявлять относительно слабые синусоиды в присутствии аддитивного случайного шума»

Вообще-то, это как раз наш случай. Слабый сигнал под шумами, несколько тонов впритирку, с разносом, скажем, 10 Hz. Надо пробовать с оконной функцией WELCH или без неё, сравнивая результат.

Динамический диапазон.

До сих пор мы смотрели картинки на генерированных данных, то есть с максимальным сигналом. От приёмника подобный сигнал получить тоже можно, но в таких условиях «цифра» и не нужна. Нужна она, когда сигнал едва проглядывается на спектре над шумовой дорожкой.

Картинка с реального приёмного тракта приведена в самом начале статьи, и шумовая дорожка с подключенной антенной там прорисовывается близко к горизонтали -50 dB. Соответственно, рабочий динамический диапазон по звуку составляет что-то около 50 dB, что не надо путать с динамическим диапазоном самого приёмника, близким к 100 dB. Разница - это работа АРУ.

Возникает вопрос, способна ли Ардуина оцифровывать сигнал, перепад уровня которого составляет как минимум 50 dB.

Формула для динамического диапазона DR в зависимости от разрядности АЦП N, который у Ардуины десятиразрядный, выглядит так:

DR [dB] = 20 * log₁₀(2^N - 1);

Предельный динамический диапазон 10-разрядного АЦП составляет 60 dB, и при грамотном засовывании звука в Ардуину всё должно получиться.

Предполагается, что вопрос о способах «грамотного засовывания звука в Ардуину» не стоит, и юзер понимает, какое напряжение выставлять на пине A0, и что именно при этом писать внутрь analogReference, дабы размах оцифровываемого звука «от пика до пика» соответствовал возможностям АЦП. Про такие вещи мы тут не будем.

Сильно зашумлённый сигнал.

Давайте поставим три тона впритирку, пусть они сменяют друг друга сперва по возрастанию, а после небольшой паузы по убыванию. Наиболее просто сгенерировать такую последовательность в аудиоредакторе OcenAudio, причём им же можно сигнал зашумить. Но поскольку правильный алгоритм зашумления неизвестен, воспользуемся утилитой PathSim:

Если скормить такой зашумлённый до SNR -25 dB сигнал связному софту FLDIGI, он его, конечно, покажет, но на фоне реальных эфирных шумов эти три полоски потеряются. Причём, если включить эмулятор ионосферного расколбаса с самыми отвязными настройками, как на картинке, то на водопаде эти три полоски можно даже не увидеть. Ежели получится детектировать такое Ардуиной Нано, оно будет за счастье.

Увидеть «три полоски» на выходе алгоритма Гёрцеля не получится:

Да, где-то какого-то цвета в верхней части шумового спектра больше, но напрямую с этим работать нельзя. Ибо форменный хаос.

Изобретение велосипеда.

Однако, если к каждому детектору тона на выходе алгоритма Герцеля применить экспоненциальное скользящее среднее, реализуемое одной строчкой и без всякого накопления и хранения данных в громоздких массивах, то что-то вменяемое разглядеть уже можно:

Тут хотя бы просматриваются разнесённые во времени, пусть и порядком размытые, но как-то локализованные тона. Правда, каждый со своим уровнем, и весьма шумоподобные. Но увидеть последовательность синий-красный-зелёный и зелёный-красный-синий теперь возможно.

Будет хорошей мыслью к этим же самым данным применить ещё по одному экспоненциальному скользящему среднему, но с кратно большим временем усреднения. Чтобы не творить на экране хаос, рассмотрим только один тон и три его кривульки, а не все девять сразу, которые местный автор видел, и впечатлился.

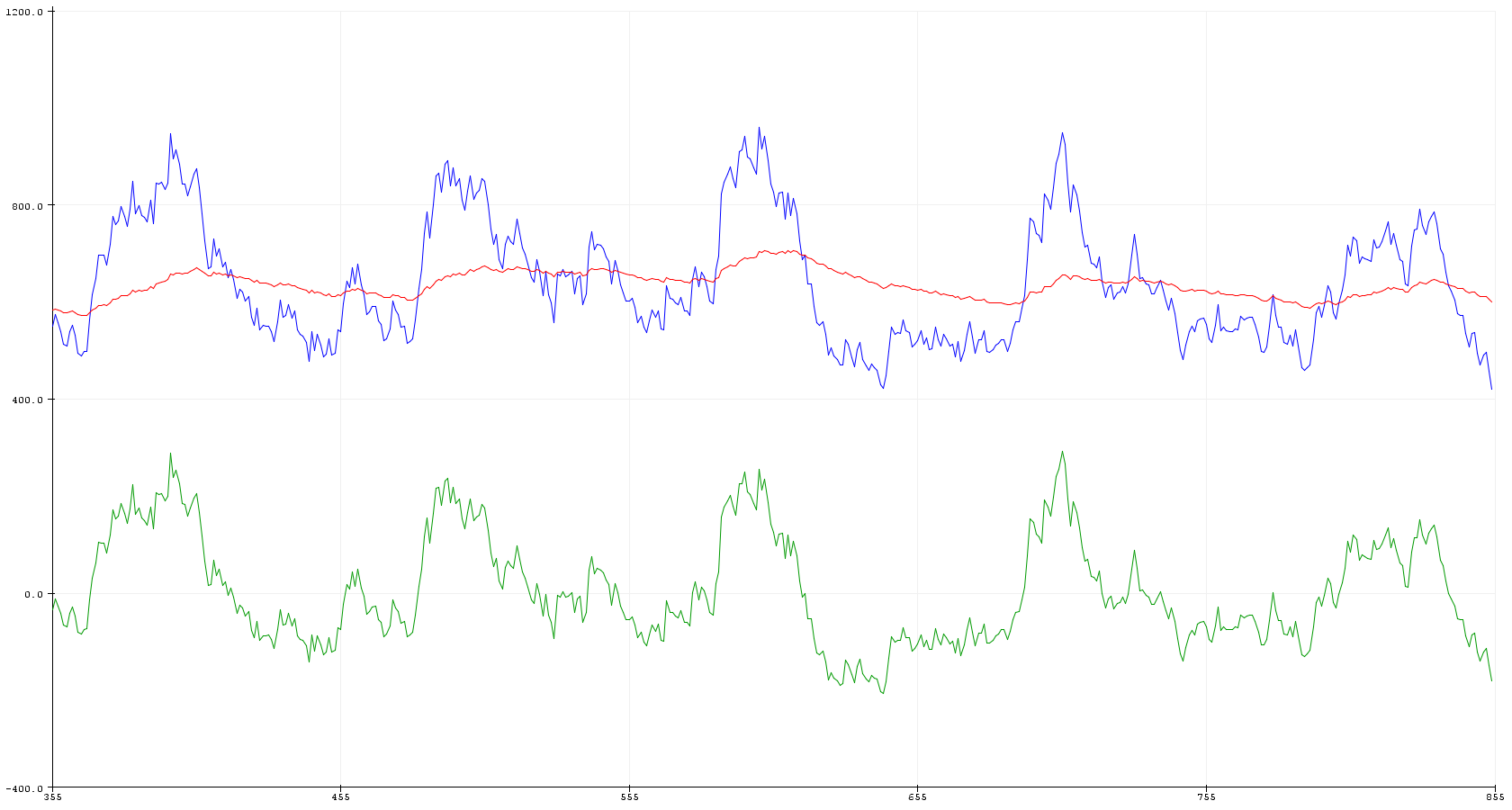
Здесь «быстрое» усреднение в виде синей линии пересекается где-то по центру красной линией, порождённой «медленным» усреднением. Если вычесть из одного другое, получится зелёная линия, колеблющаяся около нуля. Там, где она выше нуля, сигнал статистически есть.

Можно долго играться с коэффициентами скользящего среднего, получая чуть разные, но однотипные картинки. Однако смысл понятен - просто зафиксировав время достижения максимума разностной кривой для каждого тона, можно понять последовательность звучания этих тонов в эфире.

Фактически это самый простой велосипед, какой только можно изобрести. Ездит он на двух колёсах:

1. Каждая посылка должна включать все три тона, звучащие в любой последовательности. Итого всего шесть комбинаций (факториал трёх).

2. Между посылками должна быть пауза, чтобы если какой-то тон стоит последним в первой посылке, и первым во второй, в промежутке он имел возможность продемонстрировать своё отсутствие.

   Экспериментально выяснено, что длительность паузы для этого должна составлять не менее удвоенной длительности звучания тона.

При соблюдении этих двух простых условий получается что-то среднее между сверхмедленным телеграфом (который QRSS) и трёхтоновым FSK, вполне способным работать на уровне -25 dB SNR, даже при порядком покорёженном сигнале, прошедшим ионосферу.

Принципиальным тут является некоторая периодичность звучания в эфире каждого тона, пусть и немного сбитая перестановкой тонов местами в разных посылках. Только силами двух скользящих средних, без замеров и сравнений амплитуд, можно обнаружить наличие либо отсутствие тона в данный момент. Поэтому формально «велосипедный» алгоритм не особо зависит от силы сигнала.

И это хорошо, так как взаимодействие двух экспоненциальных скользящих средних, всеми силами стремящихся совпасть друг с другом, образуют нечто похожее на программную АРУ, либо нормирующий усилитель.

Шо маемо?

Все возможные комбинации трёх тонов в координатах время-частота можно графически отобразить таким образом:

Если пронумеровать частоты от 0 до 2, то их комбинация подписана снизу красным, а индекс этой комбинации сверху зелёным.

Повернув рисунок на 90 градусов по часовой стрелке, получим «водопад» связного софта, на котором переходы между тонами не будут заметны, а сами тона успешно прорисуются. Если же пользоваться специальным софтом для наблюдения QRSS «Argo», оный покажет картинку, прямо как на графике.

Получается что-то достаточно медленное, ходящее по эфиру со скоростью двух-трёх посылок в минуту, каждая из которых способна принимать шесть разных значений.

Что бы это могло быть, предстоит придумать позже. Пока же важно только одно обстоятельство: эта информация может быть принята и сохранена собственными силами самой допотопной Ардуины, без привлечения какой-либо вычислительной техники. Каковая задача тут и решается.

Область применения.

В авторском варианте код «велосипеда» на 600 отсчётов (интервал между частотами тонов 10 Hz) занял в Ардуине Нано 17% программной памяти, и 69% оперативной, скетч приводится. Туда можно дописать ещё что-то довольно-таки объёмное, но не особо требовательное к оперативке. Памяти для переменных остаётся маловато.

Ресурсов вполне хватает на поддержку дисплея, чтобы выводить на него принятые циферки от 1 до 6, которые что-то, да означают. Ежели не хочется городить дисплей, можно громко пищать принятую циферку азбукой Морзе сразу по получении, или складывать в память, чтобы пропищать потом, при нажатии кнопки.

Людям, помнящим, как выглядит пейджер, не нужно рассказывать про кодовые послания и массу ситуаций, когда такого послания достаточно :)

Другое применение, не столь очевидное, это селективный вызов.

На КВ, где шумоподавителя нет по принципиальным соображениям, пребывание на дежурном приёме мучительно. Если связь не сеансовая, звук неминуемо будет убран на минимум, чтобы оно не шумело и не трещало грозовыми разрядами. Ну и когда связь проснётся, призывно кричать она будет в выключенный динамик.

Селективный вызов весьма облегчит жизнь. Эфир можно ушами не слушать, запрограммировав приёмник на детектирование последовательности тонов. Когда она пройдёт по каналу связи, причём с уровнем, даже меньшим, чем необходимо для понимания речи, сработает какой-нибудь звонок, прямо как у телефона.

Для брутальности можно назначить две разных последовательности тонов, которые должны быть приняты друг за дружкой в течение минуты. Тут возрастает и номерная ёмкость, и защита от случайной сработки.

Эфирные испытания.

Хорошо бы придерживаться каких-то стандартов. Так, в QRSS длительность точки принята за 3 сек, и вроде людям этого хватает. Так что в коде скетча, приведённого чуть выше, длительность тона с пяти тысяч ms переправлена на три. Всё остальное должно отмасштабироваться само.

В качестве тестового сигнала редактором OcenAudio наделаны файлики тонов, которые потом склеены в три варианта их чередования, с паузами по краям в три секунды. Функция реверса позволяет из трёх файликов получить ещё три, звучащих задом наперёд, и обретаем полный комплект. Далее из шести «аккордов» можно составлять «мелодию», которая для конкретности звучит как 1-6-3 согласно предыдущего рисунка.

Этот же редактор позволил засунуть «мелодию» в левый канал mp3 файла, с уровнем -9 dB. В правый канал записан звук уровнем 0 dB, с частотой 1500 Hz. Такое извращение понадобилось из-за тестового оборудования, представленного «Волынкой», умеющей в VOX, повешенный именно на правый канал. Просто подтыкаем этой железяке на вход плеер, а дальше оно само собою управляет.

Как следует из другого материала, про связь на частотах порядка 3.6 МГц, при эмулировании связи между двумя самоделками, но с виртуальной заменой одной из них на WEB-SDR, мощность передающей железяки надо снизить на 8 dBm, в данном случае до 400 mW. Именно для этого звук в левом канале ослаблен на 9 dB, что с учётом не шибко стандартного уровня выхода плеера в итоге даёт примерно 400 mW в антенне.

Теперь, если поставить с двух сторон радиолинии однотипные железяки, но с меньшей чувствительностью по сравнению с SDR, включив их на полную мощность, то получим примерно то же самое, что и в этом тесте.

Ближайшие WEB-SDR всё равно увидели слишком большой сигнал, с дешифровкой которого у Ардуины проблем не возникает, но и ничего не даёт. Поэтому был найден SDR в 800 км, принимающий 400 mW на грани видимости сигнала глазом на «водопаде». Есть скрин, в который надо кликнуть:

Тонюсенькой красной стрелочкой над водопадом показана вертикаль, на которую нужно смотреть, чтобы узреть следы сигнала. Конкретно тут он на 20 dB ниже шумов, ибо алгоритм Гёрцеля демонстрирует ну очень большие пики по сравнению с теми, что наблюдаются в лабораторных условиях при SNR - 25 dB, то есть запас по чутью ещё велик.

Вертикальные выбросы различной высоты у линии оранжевого цвета обозначают номера продетектированных «аккордов». Способа тупо вывести цифру на график местный автор не нашёл.

Оконные функции.

Эксперименты с оконными функциями усердно проводились, но так и не дали никакого ощутимого результата. Вероятно, можно обойтись и без них.

Что может быть нехорошо?

Смутить нас может только диалектика - как правило, одно достигается за счёт другого. В данном случае узкая полоса приёма для кажого тона обеспечивает отличную чувствительность под шумами. Вопрос только в том, совпадут ли до Герца частоты двух радиостанций.

Действительно, несовпадение частот настройки двух железяк всего на ½ от SLR (спектрального разрешения, у нас 10 Hz) помещает сигнал посерёдке между каналами анализатора по Гёрцелю, и с этим что-то придётся делать. Реальная стабильность частоты должна составлять ¼ от SLR, причём не на протяжении сеанса, а долговременно.

По всй видимости, было бы слишком оптимистично ожидать от самодельной железяки отклонение частоты от сетки не более 2 Hz во всём возможном температурном диапазоне. Опыт по изобретению железяк говорит, что в них уход частоты только при самопрогреве соизмеримый.

Положение не спасает даже применение такой высокотехнологичной штуки, как синтезатор. В котором термостатированный кварц - весьма вычурная экзотика, и в итоге кварцевый генератор на транзисторе может оказаться более стабильным, нежели синтезатор.

Поэтому при реальном применении декодера имеет смысл (более фатальная формулировка - придётся) выбрать SLR вдвое больше, 20 Hz. Уход относительно сетки на ± 5 Hz фактически никак не повлияет на работу декодера. Обеспечить такую долговременную стабильность в самодельной железяке уже видится возможным.

В скетче на этот раз алгоритм Гёрцеля запущен по учебнику, потому как используется всего 300 отсчётов, и всё шевелится весьма шустро. Скетч занимает 21% памяти программ, и 42% динамической памяти, оставляя больше места для чего-то ещё. Тона назначены стандартно, в границах телеграфного фильтра (580, 600, 620 Hz), да и к тому же ухо слышит эти частоты лучше всего.

Лабораторные исследования показали принципиальную работоспособность с сигналом на 25 dB ниже уровня шума при полосе 3 kHz и спектральном разрешении 20 Hz, однако активные эфирные помехи смоделировать нечем. Проверяем, будет ли оно работать в реальном эфире.

Дневной тест проведён на 300 км в 15 часов по местному времени, когда связь зенитным излучением наиболее затруднена. Тем не менее, она есть, и выходную мощность железяки пришлось дополнительно уменьшить до 250 mW, чтобы не кричала слишком громко:

Красной стрелочкой отмечено место, где следует искать сигнал. SDR с очевидностью стоит мимо сетки, причём с ошибкой, не кратной 10 Hz, а позиционироваться можно лишь с шагом 10 Hz, но теперь это не мешает. При 600 отсчётах настроиться точно на этом ресурсе было невозможно.

Сохранилась ли возможность связи на 800 км? Да, причём это даже не сумеречная, а почти дневная связь (в 17.30 по локальному времени в это время года ещё светло):

Однако величина пиков над нулём падает до ~200 попугаев, что близко к пределу чувствительности.

Что может быть действительно нехорошо.

Безусловно, со своим QRP, и особенно связью через зенитное излучение, мы будем сильно обломаны периодическими затуханиями, «качающими» сигнал порою на десятки dB, и уводящими его в полную нечитаемость (QSB).

По-научному связь в таких условиях называется «Релеевский канал». Тут можно подождать открытия прохождения, либо поднять мощность, чтобы QSB роняли уровень сигнала до отметки SNR не ниже способностей к дешифровке используемой «цифры».

Лечатся такие вещи только размазыванием полезной информации по всей длительности передачи, с внесением в неё многократно избыточного кода, обладающего свойствами самокоррекции. Либо увеличением длительности звучания тона сверх среднестатистической длительности замираний.

Но наш велосипед предельно простой для таких заморочек.

Уместные размышления.

Максимальное упрощение программного детектора тонов в эфире, а именно, оперирование для каждого из тонов парой скользящих средних с чуть различающимся временем накопления, хоть и позволяет легко получить самотактирующийся по паузам детектор, но у него есть ограничения. Если сигнал черезчур зашумлён или сильно федингует, все три разностных кривых могут не уйти ниже ноля, и пауза не наступит.

Мысль заменить паузу на четвёртый тон, звучащий вместо неё, может оказаться перспективной.

Что-то более практичное.

Как оказалось, мало кто умеет в Ардуину, поэтому чуть позднее пришлось дописать ещё несколько демонстрационных скетчей.

Будем исходить из представлений о прекрасном конкретно местного автора. Вот любит он оснащать свои железяки четырёхразрядным индикатором, которого вроде бы для всего хватает. Пускай код дистанционной активации девайса (пока абсолютно неважно, что под этим понимается) состоит из 2-3-4 символов, которые с этого индикатора и задаются.

Ежели так, то можно договорится, что ноль в любом разряде индикатора ничего не значит, а вот циферка от 1 до 6 пусть будет «шестисмысловым битом». Передаются или принимаются они так, как отображает индикатор - слева направо, по принципу бегущей строки.

Допишем предыдущий скетч парочкой примитивов, и условимся, что в переменной signature содержится число из циферок от 0 до 6, причём нули не значащие, и призваны варьировать разрядность. Фактически это и есть шестисмысловые биты с индикатора без какой-либо обработки.

Этот скетч внимательно слушает звук на пине A0, и при наличии там посылок, пронумерованных на графике в статье как 1-6-3-5, реагирует морганием встроенного на плату Ардуины светодиодика.

Местный автор полагает, что в реальности при получении по эфиру оговоренной индикатором кодовой посылки железяка должна перейти на передачу, и ответить каким-то другим кодом состояния, который что-то значит, и может меняться. Это соответствует процедуре проверки связи, и передаче своего статуса, которому лучше бы быть «всё в порядке», но в жизни случается всякое.

Можно помыслить в иную сторону.

Далеко не все способны оперировать абстракцией «шестисмысловой бит», и понятия не имеют, что с ним делать. Это можно понять, нормальные люди никаких систем счисления, кроме десятичной, не знают. И знать не хотят.

Тогда берём в руки другой скетч, в котором переменная signature теперь десятичная, и соответствует числу на четырёхразрядном индикаторе от 0 до 1295. Где-то там внутри число с индикатора переводится в шестеричное от 0 до 5555, но чтобы свести задачу к предыдущей, к каждому разряду мы добавим единицу, перейдя в диапазон 1111-6666. Далее это сравнивается с последовательностью «шестисмысловых битов», принятых по эфиру.

Тут от переменной разрядности пришлось отказаться, но зато привычный десятичный диапазон индикатора 0000-1295 позволяет более осмысленно кодировать информацию, нежели в шестеричной системе счисления. И, по большому счёту, даже и не важно, как именно устроена транспортировка циферок по эфиру. Берём десятичное число из указанного диапазона, и передаём силами пары Ватт километров на пятьсот ровно за минуту, с автоматическим приёмом на той стороне, и даже, возможно, также автоматическим реагированием на весточку.

Можно, конечно, пойти дальше, и вместо трёх тонов использовать четыре, перейдя от шестеричной системы к 24-теричной. Однако, кроме как с конвертацией в привычную десятичную систему счисления, с этим работать решительно невозможно, так что бодаться с такими сущностями мы не будем. Лучше упороться по какому-нибудь другому поводу.

На тот случай, если захочется распознавать не фиксированный код, а несколько разных, заданных массивом, такое тоже можно, причём как для шестеричных, так и десятичных кодов. Но от переменной разрядности придётся окончательно отказаться, мессидж будет в четыре аккорда.

Про десятичное и шестеричное.

Некоторое недоумение может возникнуть по поводу того, зачем местный автор разрывается между двумя системами счисления. Ну да, челендж понятен - прерывистая мелодия должна звучать в эфире не дольше минуты, своими прерываниями сама себя структурируя, в результате чего мы должны получить, к примеру, какие-то циферки на дисплей.

Если разрядность дисплея четыре, то в каждом разряде будет циферка из диапазона 1-6 для шестеричного представления, или число от 0 до 1295 для десятичного варианта (те же самые 6⁴).

Люди, использующие радиосвязь строго по делу, тут же узрели возможность применить Ten-коды, либо ещё какие-то аналогичные, но менее известные системы. Или даже несколько сразу. Табличку на 1000 с лишним клеток не так-то просто заполнить.

С другой стороны, для нужд телеметрии вполне достаточно и четырёх параметров, у каждого из которых есть пять состояний, либо градаций (шестое состояние пусть включает какую-то другую логику). На примере туристов это могут быть такие пункты, как здоровье, погодные условия, припасы, продвижение по маршруту. Достаточно каждый пункт оценить по шкале от 1 до 5, к чему мы все приучены со школы, и такой информации хватит. Всё предельно просто и наглядно.

Хорошо, когда есть разные варианты.

Об информационной ёмкости.

Конечно, нужно разделять случаи ожидания приёма вполне определённой последовательности (селективный вызов), и наперёд неизвестной. Хитрые переплетения трёх пар скользящих средних в условиях эфирных помех и особенно при серьёзно федингующем сигнале, способны запутаться, и в растерянности от вдруг случившегося свингерства исказить передаваемую информацию.

Из-за низкой разрядности тут вряд ли можно применить код Хэмминга и всевозможные вариации на эту тему. А вот контрольную сумму вполне удастся. Например, алгоритм Ханса Луна, либо ещё что-то столь же простое в реализации для шестеричной системы счисления.

Контрольный код скушает один разряд, так что останется 6³=216 значений.
Хотя это не всегда и не совсем так.

Тестовый скетч алгоритма Луна к трём разрядам кода из диапазона 111-666 приписывает спереди контрольную сумму, вычисляемую стандартно, но адаптированную под шестеричную систему. И вроде бы число значений от этого не меняется, но местный автор обнаружил перспективный лайфхак.

Если подсунуть алгоритму в качестве начального значения переменной, в которую суммируются разряды, не ноль, а любую цифру от 1 до 5, разряд контрольной суммы тоже получает смещение. Это означает, что имеется шесть самостоятельных «пространств Луна» ёмкостью 6³, с одинаковыми младшими разрядами, но различающимся старшим (табличка состояний в архив вложена).

Суммарная ёмкость всех пространств составляет в точности 6⁴.

Поскольку дешифратор, проверяющий контрольную сумму, отвергнет всё не попавшее в его пространство, возникает годная возможность направленной передачи, по аналогии с селективным вызовом. Это похоже на радиосвязь с субтоном, когда радиостанция произносит вслух только то, что передаётся с известным ей кодом на подтональных несущих.

Работает всё это совершенно предсказуемым образом, скетч приводится. При детектировании кодов из своего «пространства Луна» Ардуина моргает светодиодом, и складывает кодовые посылки в массив. Так как у местного автора был заготовлен тестовый звуковой файлик, попадающий во второе «пространство Луна», оно в коде и выбрано, будьте внимательны.

А теперь настало время упороться.

Ежели всё-таки хочется информационной ёмкости побольше, можно закрыть гештальт с 24-теричной системой счисления, и использовать «аккорд» из четырёх тонов. Если постараться уложиться в минуту, это обернётся тремя аккордами, первый из которых будет контрольной суммой к двум другим. Тогда доступно 24²=576 позиций, и оперировать с ними придётся только в десятичном виде.

Скетч, аналогичный предыдущему, также с алгоритмом Луна на борту, но в 24-теричной системе счисления, прилагается. Частоты четырёх тонов прописаны в скетче, они образуют довольно много комбинаций (4!=24). Таблица соответствия контрольной суммы двум 24-теричным разрядам в архиве есть.

Так же как и в предыдущем случае, для разных «пространств Луна» табличка будет своя, и формально можно говорить об информационной ёмкости в 24³, или 13824 состояниях. Но поскольку на четырёхразрядном индикаторе правые три разряда заняты отображением номера сообщения от 0 до 575, на старшем разряде логично выставлять также десятичную циферку от 0 до 9, работая только с частью «пространств Луна».

Следует отметить, что в шестеричном варианте усреднённая скважность у тонов составляла ⅕, в 24-теричным уменьшилась до ⅙. И к сожалению, это повлекло уменьшение предельной чувствительности на пару dB. Но тут диалектическое противоречие, оно миром не решается.

Коллизии.

Выдумывая алгоритм, обслуживающий транзит байтов в нестационарной среде, нужно быть готовым к потере или порче этих самых байтов. Чтобы не сталкиваться с эффектом «испорченного телефона», когда посылается один набор кодов, а получается совсем другой.

Давайте посмотрим на картинку.

Цифрой 1 обозначена посылка из 4 тонов в самой последней модификации с 24-теричной логикой. Чтобы передать десятичный код в диапазоне 0-575 с контрольной суммой, нужно поставить три таких посылки друг за дружкой впритирку (строчка 2, все последовательности тонов условно одинаковые. Пустая клетка - это пауза длительностью в один тон).

Предположим, что следом за этим кодом необходимо послать ещё один (строка 3). Итоговая комбинация выглядит, как обозначено строкой 4.

Допустим, что несколько тонов из этой последовательности выпали, не смогли приняться (строка 5). И формально возможна ситуация, когда тоновые последовательности разных кодов скомбинируются во вполне легитимный (выделено жёлтым фоном), если в данном случае последняя посылка первого кода подойдёт в качестве контрольного кода к первым двум посылкам второго кода. Вероятность такого события низкая, но не невозможная.

Очевидно, необходимо разделять коды дополнительной паузой, нарушая тем самым периодичность следования тоновых посылок. Если перед каждым кодом формировать паузу стандартной длительности, и добавлять такую же после кода, проблема на том и порешается.

Теперь, если посчитать квадратики, и помножить каждый на 3 секунды, получим ровно одну минуту для передачи полного кадра одного кода. Соответственно, два кода подряд (строка 6) будут передаваться две минуты. Теперь без коллизий.

Вывод.

По результатам изысканий так получается, что две двух ваттных железяки вполне способны переговариваться между собой, будучи разделёнными на сотни километров, при этом для передачи и дешифровки полученного сигнала используя лишь небогатые ресурсы Ардуины Нано.

Темп в четыре шестисмысловых посылки в минуту уже достаточен для такого общения. Какой именно метод работы с каждым «шистисмысловым» битом будет выбран, в рамках этой публикации не рассматривается.

В заключение автор выражает благодарность всем, кто поддерживает работоспособность WEB-SDR приёмников, лишь благодаря которым имеется возможность выдумывать разные прикольные штуки.

Заменяем Баофенг Кваншенгом. Уже можно.

Удивительное дело, но с момента массового прихода доступной радиосвязи в широкие народные массы как-то незаметно прошло десять лет. Местный автор в меру своих сил и способностей поучаствовал в этой вакханалии, породив две нетленки про Обзор BaoFeng UV-5R и его дальность связи с разными антеннами.

Космическое время из USB донгла.

Если человек правильно выстроил свою жизнь, он даже может не носить часов. Вот просто всё равно, сколько именно сейчас времени. Но так бывает не всегда. К примеру, все современные цифровые моды дальней КВ связи, по которым местный автор периодически прикалывается, работают исключительно в таймфреймах.

Антенна из стального оцинкованного канатика.

Какое-то время назад местный автор проектировал дипольную антенну на 80-метровый диапазон, но питаемую с края. Речь про это дело заходила здесь, а для чего нужна именно такая штука, тоже понятно. Нет ничего более удобного и неприхотливого, нежели длинная верёвка с разъёмом на конце.

№ 1Селективный вызов на КВ - отлично!

Шумы эфира иногда выносят мозг почище любой жены, а ожидание длится вечно. Кого-то это убаюкивает и он засыпает сладким сном, прозевав всю самую мякотку.

Поэтому, когда прочёл о такой возможности - возрадовался, самоделки теперь можно ставить в дежурный режим и ждать "звонка", предваряющего сеанс связи. Что уже облегчает задачу тому, кто и так не высыпается.

Про сообщения "на пейджер", с мозгами в виде Ардуино Нано с индикатором и несколькими кнопками и больше ничем из гаджетов (ни компьютера, ни смартфона, красотища), разговор отдельный, тут поле непаханое. Особенно порадует потребление, если ранее надо было таскать добрый аккумулятор, то теперича на приёме мизер, а на передаче в два Ватта чуть поболее, но не так критично.

Выживальщики аплодируют стоя.
Премного благодарен, Мастер!

nextman

№ 2Подтверждаю, скетч селективного вызова работает.

Залил крайний скетч в Ардуино Нано, выставил громкость на плеере в пять делений, громкость звуковой карты такая же - пятёрочка.

При проигрывании звукового файла из архива встроенный светодиод Ардуино моргает один раз, что является доказательством совпадения значения, прописанного в скетч(543) и принятого в виде звукового сигнала.

Теперь надо проверить в эфире.

nextman